Багато хто думає, що математика – це винахід людини . Для цього способу мислення математика подібна до мови: вона може описувати реальні речі в світі, але вона не «існує» поза розумом людей, які її використовують.
Але піфагорійська школа думки в стародавній греції дотримувалася іншого погляду. Його прихильники вважали, що реальність в основі своїй математична.
Через більше 2000 років філософи і фізики починають серйозно ставитися до цієї ідеї.
У новій статті сем барон, доцент австралійського католицького університету, стверджує, що математика – це важливий компонент природи, який структурує фізичний світ.
бджоли у вуликах виробляють гексагональні стільники. Чому?
Згідно з математичною гіпотезою про стільники, шестикутники-найефективніша форма для мозаїки площини. Якщо ви хочете повністю покрити поверхню плиткою однакової форми і розміру, зберігаючи при цьому мінімальну загальну довжину периметра, використовуйте шестикутники.
Чарльз дарвін припустив, що бджоли еволюціонували, щоб використовувати цю форму, тому що вони виробляють найбільші клітини для зберігання меду і найменшої кількості енергії для виробництва воску.
Гіпотеза про стільники була вперше запропонована в стародавні часи, але була доведена тільки в 1999 році математиком томасом хейлзом.
цикади і прості числа
Ось ще один приклад. Є два підвиди північноамериканських періодичних цикад, які більшу частину свого життя живуть в землі. Потім кожні 13 або 17 років (в залежності від підвиду) цикади з’являються великими зграями протягом приблизно двох тижнів.
Чому 13 і 17 років? чому не 12 і 14? або 16 і 18?
Одне з пояснень апелює до того факту, що 13 і 17 – прості числа.
Уявіть, що у цикад є ряд хижаків, які також проводять більшу частину свого життя в землі. Цикадам потрібно вилазити з землі, коли їх хижаки сплять.
Припустимо, є хижаки з життєвим циклом 2, 3, 4, 5, 6, 7, 8 і 9 років. Як найкраще їх усіх уникнути?
вгорі: p1-p9 представляють цикл хижаків. Числова лінія представляє роки. Виділені прогалини показують, як 13-і 17-річним цикадам вдається уникати своїх хижаків. Сем барон
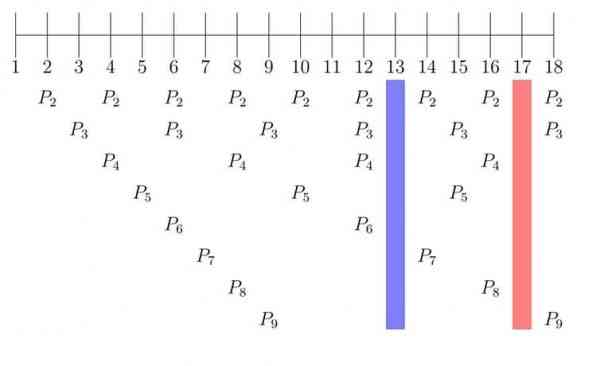
Порівняйте 13-річний життєвий цикл і 12-річний життєвий цикл. Коли цикада з 12-річним життєвим циклом виходить з-під землі, 2-річні, 3-річні і 4-річні хижаки також вилітають з-під землі, тому що 2, 3 і 4 всі діляться на 12 порівну.
Коли цикада з 13-річним життєвим циклом виходить з-під землі, жоден з її хижаків не вилізе з-під землі, тому що жоден з 2, 3, 4, 5, 6, 7, 8 або 9 не ділиться рівномірно на 13. Те ж вірно і для 17.
Схоже, ці цикади еволюціонували, щоб використовувати основні факти про числа.
створення або відкриття?
Як тільки ми почнемо шукати, легко знайти інші приклади. Від форми мильних плівок до конструкції шестерень в двигунах, розташування і розміру зазорів в кільцях сатурна – математика всюди.
Якщо математика пояснює так багато всього, що ми бачимо навколо, то малоймовірно, що математика-це те, що ми створили. Альтернативою є відкриття математичних фактів: не тільки людьми, але і комахами, мильними бульбашками, двигунами внутрішнього згоряння і планетами.
що думав платон?
Але якщо ми щось відкриваємо, що це таке?
У давньогрецького філософа платона була відповідь. Він думав, що математика описує реально існуючі об’єкти.
Для платона ці об’єкти включали числа і геометричні фігури. Сьогодні ми можемо додати до списку більш складні математичні об’єкти, такі як групи, категорії, функції, поля і кільця.
Платон також стверджував, що математичні об’єкти існують поза простором і часом. Але такий погляд тільки посилює загадку того, як математика що-небудь пояснює.
Пояснення включає в себе демонстрацію того, як одне в світі залежить від іншого. Якщо математичні об’єкти існують у царстві, відмінному від світу, в якому ми живемо, вони, схоже, не можуть мати відношення до чого-небудь фізичного.
увійдіть до піфагореїзму
Стародавні піфагорійці погоджувалися з платоном в тому, що математика описує світ об’єктів. Але, на відміну від платона, вони не думали, що математичні об’єкти існують за межами простору і часу.
Замість цього вони вважали, що фізична реальність складається з математичних об’єктів так само, як матерія складається з атомів.
Якщо реальність складається з математичних об’єктів, легко побачити, як математика може зіграти роль в поясненні світу навколо нас.
За останнє десятиліття два фізика виступили на захист піфагорійської позиції: шведсько-американський космолог макс тегмарк і австралійський фізик-філософ джейн макдоннелл.
Тегмарк стверджує, що реальність – це лише один великий математичний об’єкт. Якщо це здається дивним, подумайте про те, що реальність-це симуляція. Моделювання-це комп’ютерна програма, яка являє собою свого роду математичний об’єкт.
Погляди макдоннелла більш радикальні. Вона думає, що реальність складається з математичних об’єктів і умів. Математика-це те, як всесвіт усвідомлює себе.
Автор захищає іншу точку зору: світ складається з двох частин: математики і матерії. Математика надає матерії її форму, а матерія надає математиці її сутність.
Математичні об’єкти забезпечують структурну основу для фізичного світу.
майбутнє математики
Логічно, що піфагореїзм заново відкривається у фізиці.
У минулому столітті фізика ставала все більш і більш математичною, звертаючись до, здавалося б, абстрактних областей досліджень, таких як теорія груп і диференціальна геометрія, в спробі пояснити фізичний світ.
Оскільки межа між фізикою і математикою стирається, стає все важче сказати, які частини світу є фізичними, а які – математичними.
Але дивно, що філософи так довго нехтували піфагореїзмом.
Барон вважаю, що це скоро зміниться. Настав час піфагорійської революції, яка обіцяє радикально змінити наше розуміння реальності.
Нагадаємо, раніше повідомлялося, що були названі лауреати абелівської премії 2021.
